研究内容

■量子現象（主にトンネル現象）の時間スケールとそれに関連した諸問題
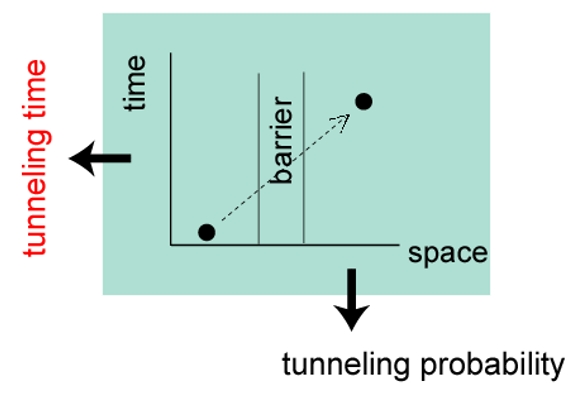
　壁にボールをぶつけると跳ね返りますが、量子力学が支配するミクロな世界では ボールは壁を壊すことなくすり抜けることがあります。これをトンネル効果と言います。 量子力学的な粒子がトンネル効果によってエネルギーの壁を通り抜けるのに要する時間は 「トンネル時間」と呼ばれ、理論的・実験的に大きな関心がもたれています。
　これまでに様々なトンネル時間が提案されていますが、山田は、それらのうち 透過振幅の微分で求めることができる４つのトンネル時間が、ある統一的な方法で 導出できることを以前示しています （Phys. Rev. Lett. 93, 170401 (2004)）。
　近年、原子のトンネルイオン化の実験によりトンネル時間を測定したという報告がいくつかなされ、 トンネル時間に対する関心が再び高まっています。また、トンネル現象を利用したメモリ では、メモリの書き込み時間が障壁の幅にどのように依存するのか、という点が重要です。 この時間は必ずしもトンネル時間というわけではありませんが、こうした時間も 含め、トンネル現象に関係した時間スケールを明らかにする研究を行っています。
　卒業研究や修士論文研究の場合には、量子力学的な粒子の運動を数値シミュレーション を用いて解析することによって、こうした課題に取り組むことになります。

■時間に依存したシュレーディンガー方程式の近似解析解
　時間に依存したシュレーディンガー方程式は、量子力学を構成する2本の柱のうちの1つです（もう1つは ボルンの確率解釈）。一般的には、この方程式を解析的に解く（答を式の形で得る）ことは 不可能なため、数値的に解く（答を数値として得る）ことが通常行われます。しかし、対象とする 系（システム）の性質について確定的な結論を得るためには、数値解では「力不足」であることも 少なくありません。このため、何らかの近似を導入して解析的に解く（近似解析解を求める）研究が いろいろと行われています。
　当研究室でも、入射波束が幅の広いガウス型で、ポテンシャルが静的かつ有限領域におさまっている 場合に、透過波束の近似解析式を得ています（ 日本物理学会2008年秋季大会20pVD-2）（※）。この近似解析式を用いると、波動関数（時間に依存したシュ レーディンガー方程式の解）の時間変化を非常に手軽にシミュレーションできるだけでなく、数値計算のみでは 突き止めることが難しい波動関数の詳細な性質も知ることができます。現在、この近似解析式の 精度向上、適用可能範囲拡大の研究に取り組んでいます。
　卒業研究や修士論文研究の場合には、近似解析解と数値シミュレーションによって得られた結果を 比較することを通して、こうした課題に取り組むことになります。
（※）最近出版された量子力学のテキストの中で、上記近似解析解が 紹介されています。

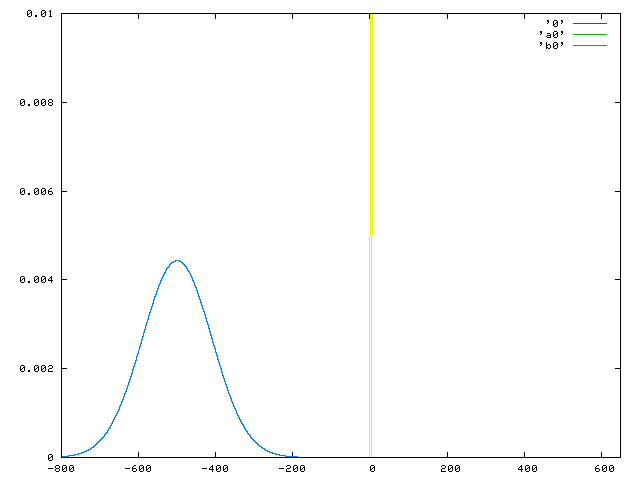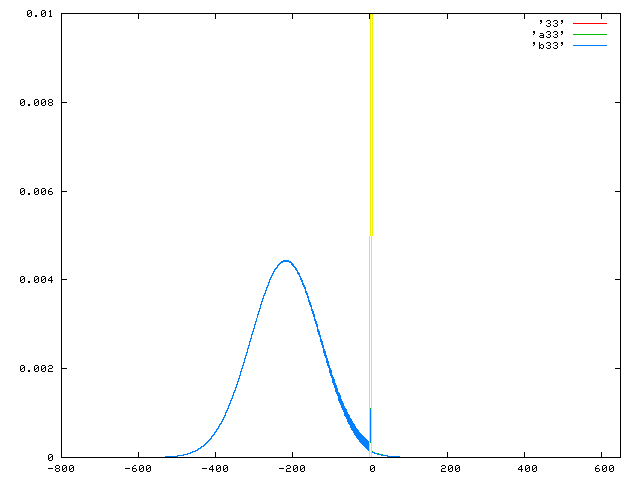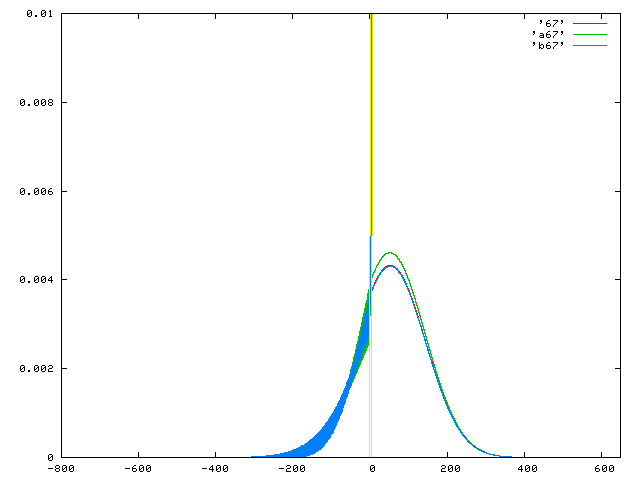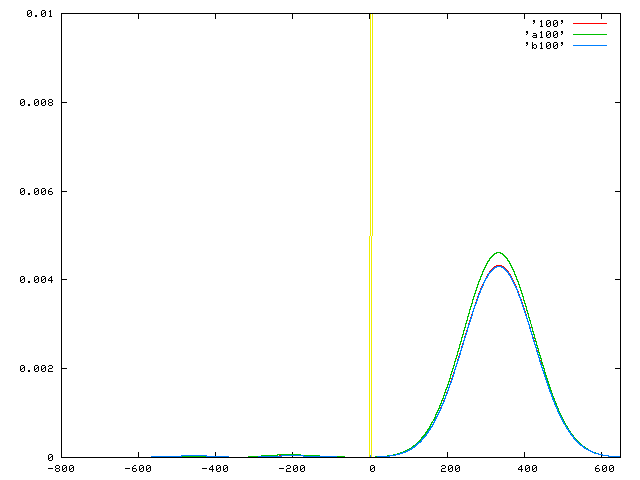　赤:数値解、緑：0次近似解、青：2次近似解

■格子上の経路和法（離散的なpath integral）とそれに関連した諸問題
　量子力学の形式の一つに「経路積分法」があります。これは、ある地点から別の地点に行く確率振幅を、 二点を結ぶ全ての経路にわたって複素確率を足しあげることによって求める方法です。これはファインマンによって 定式化されましたが、「経路に関する足し上げ」が「無限多重積分」という複雑な仕掛けによって表現されており、「もっと素朴な表現の経路和 で済ますことはできないか？」という疑問が湧いてきます。実際、相対論的量子力学（ディラック方程式、1+1次元）の場合には、 格子時空上の離散的経路和によって、経路を一本一本足すという素朴な方法で確率振幅が正しく求まります。これは ファインマン自身が教科書の中で述べています （Feynman and Hibbs, Quantum Mechanics and Path Integrals (1965), Problem 2-6）。シュレーディンガー 方程式の場合にも同様なことができないか前から気になっていましたが、ようやく最近それが可能であることが わかりました（日本物理学会2017年秋季大会 22aJ25-10）。この問題は量子ウォーク（ランダムウォークの量子力学版）とも関連しており、またベッセル関数の高精度な 漸近展開という点からも面白く、引き続き研究を進めています。

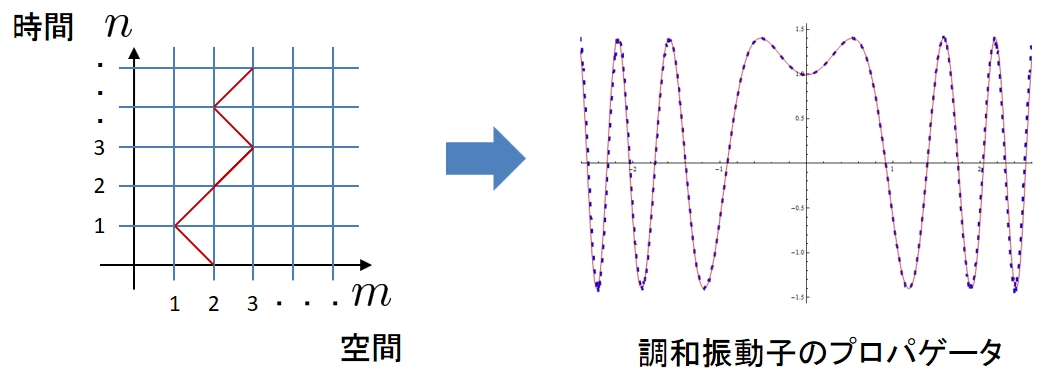　赤:解析解、青：格子上の経路和

■Consistent histories approach to quantum mechanics
　ミクロな世界では、全く同じ状態の粒子が複数あっても、物理量（粒子の位置、運動量、エネルギーなど）の測定結果は 粒子ごとに異なるのが普通です。量子力学は、こうしたミクロの世界を、確率を用いて記述します（粒子が位置Aの周辺に 見出される確率がいくら、位置Bの周辺に見出される確率がいくら、といった具合に）。確率論の観点から見たときの量子力学の大きな特徴は 「ある瞬間の出来事に対してのみ確率を付与する」ということです（複数の瞬間に関係した出来事であっても、各瞬間 の事象に還元できるものであれば同じこと）。さて、古典力学の法則に従う質点に対しては“first hitting time” を考えることができます。これは、空間のある定められた点を質点が初めてhitする時刻のことです。 古典的な確率論に従う粒子集団に対しては first hitting time の確率分布を考えることができます。しかし、 量子力学的な粒子集団に対してそれをどのように考えてよいのか、そもそもそうしたものが定義できるのか、 は自明ではありません。通常の量子力学の枠組みの中には、「t=t1からt=t2の間に粒子が初めてx=aをhitする」 という「一定時刻に縛られない事象」の確率をどのように考えたらよいのかについて、明確な処方箋は見当たらないのです。
　山田は、かつて、一定時刻に縛られない事象に対して量子力学的な確率を矛盾無く定義できる理論的な枠組みを 研究していました（※※）。そのような枠組みは、当時複数の研究者が考えており、今日それらは“consistent histories approach” や“decoherent histories approach”と呼ばれています。このアプローチの中で重要な役割を果たすものに「非干渉汎関数」 があります。これは、事象間の量子力学的な干渉の度合いを表すものです。先に、「４つのトンネル時間をある統一的な 方法で導出した」と書きましたが、それは「非干渉汎関数を用いて定義される擬平均を計算する」という方法です。 その後、トンネル時間の擬平均が、弱測定理論で計算される「弱値」と 一致することを知り、“consistent histories approach”と弱測定理論の関係にも関心を持っています。 この方向の研究も興味深いと思います。

卒業研究・修士論文研究について

教育活動のページをご覧ください。

成果の公表

学会発表や論文等を通して、研究成果の公表を行っています。

・Masaki Tsuchiya and Norifumi Yamada, Novel numerical method for charging characteristics of electron in Direct Tunneling Memory type potential, Proceedings of The 36th JSST Annual Conference: International Conference on Simulation Technology, pp. 202-205 (2017).

・Y. Kubo and N. Yamada, Charging and discharging characteristics of a quantum well with an initially Lorentzian wave packet incident on a DTM type potential, Communications in Computer and Information Science 63, pp. 118-128 (2016).

・Shun Ando and Norifumi Yamada, Wave packet tunneling through an oscillating barrier and tunneling times, Proceedings of the Joint 13th Asia Pacific Physics Conference and 22nd Australian Institute of Physics Congress. No.275 (2016).

・Y. Kubo and N. Yamada, Numerical Simulation of Quantum Buildup and Decay Processes with a Lorentzian Wave Packet Incident on a DTM Type Potential, Proceedings of the 15th Asia Simulation Conference, pp. 54-61 (2015).

・H. Azuma and N. Yamada, Efficient simulation method for quantum build-up and decay processes in resonant tunneling, Proceedings of The 34th JSST Annual Conference: International Conference on Simulation Technology, pp. 402-405 (2015).

Y. Kubo and N. Yamada, Novel method for simulating quantum buildup process in the potential well of a DTM type potential, Proceedings of The 33rd JSST Annual Conference: International Conference on Simulation Technology, pp. 70-71 (2014).

N. Yamada, Effect of the pole of the transmission amplitude on the left tail of the transmitted wave packet, 日本物理学会 2021年秋季大会, 21aL2-7 (2021).

山本 貴之，山田 徳史, ポテンシャル障壁のコーティングがトンネル特性に及ぼす影響, 2021年度電気・情報関係学会北陸支部連合大会 D-3 (2021).

武藤 健太朗，山田 徳史, 波数空間における重ね合わせを用いた近似波動関数, 2021年度電気・情報関係学会北陸支部連合大会 D-4 (2021).

N. Yamada, Wave packet tunneling through oscillating barriers II, 日本物理学会 第 76 回年次大会,15aL2-3 (2021.3).

深見 昂平，山田 徳史, 三角障壁を透過した量子波束に対する二つの近似解析式の精度の比較, 2020年度電気・情報関係学会北陸支部連合大会 D-2-2 (2020).

山本 貴之，山田 徳史, 障壁のコーティングが透過特性とDTMの充放電特性に及ぼす影響, 2020年度電気・情報関係学会北陸支部連合大会 D-2-5 (2020).

深見 昂平，山田 徳史, 時間に依存したシュレーディンガー方程式の近似解析解の精度, 2020年電子情報通信学会総合大会 C-15-29 (2020).

深見 昂平，山田 徳史, 三角障壁を透過した波束に対する近似解析式の有効性, 2019年度電気・情報関係学会北陸支部連合大会 D-4 (2019).

山藤 裕也，山田 徳史, 三角ポテンシャルにおける位相時間の解析, 2018年度電気関係学会北陸支部連合大会 D-4 (2018).

寺脇 智紀，山田 徳史, 三角DTM構造における電子の充放電特性, 2018年度電気関係学会北陸支部連合大会 D-5 (2018).

N. Yamada, Non-relativistic counterpart of Problem 2-6 in Feynman and Hibbs, 日本物理学会2017年秋季大会講演概要集第72巻第2号, p. 2468 (2017).

佐々木 真帆，山田 徳史, 新しいハートマン効果の持続距離拡大に関する研究, 2017年度電気関係学会北陸支部連合大会 D-13 (2017).

山田 徳史，安土 隼, 波束が振動ポテンシャルに入射した場合の透過確率の振動周期依存性, 日本物理学会 第71回年次大会講演概要集第71巻第1号, p. 2798 (2016).